概要

Visual FCL（Fully Connected Layer、総結合層）は、ニューラルネットワークの総結合層の学習進行を視覚的に表現するためのアプリケーションです。このアプリケーションにより、ニューラルネットワークのパラメータの学習進捗状況を目視することが可能となります。

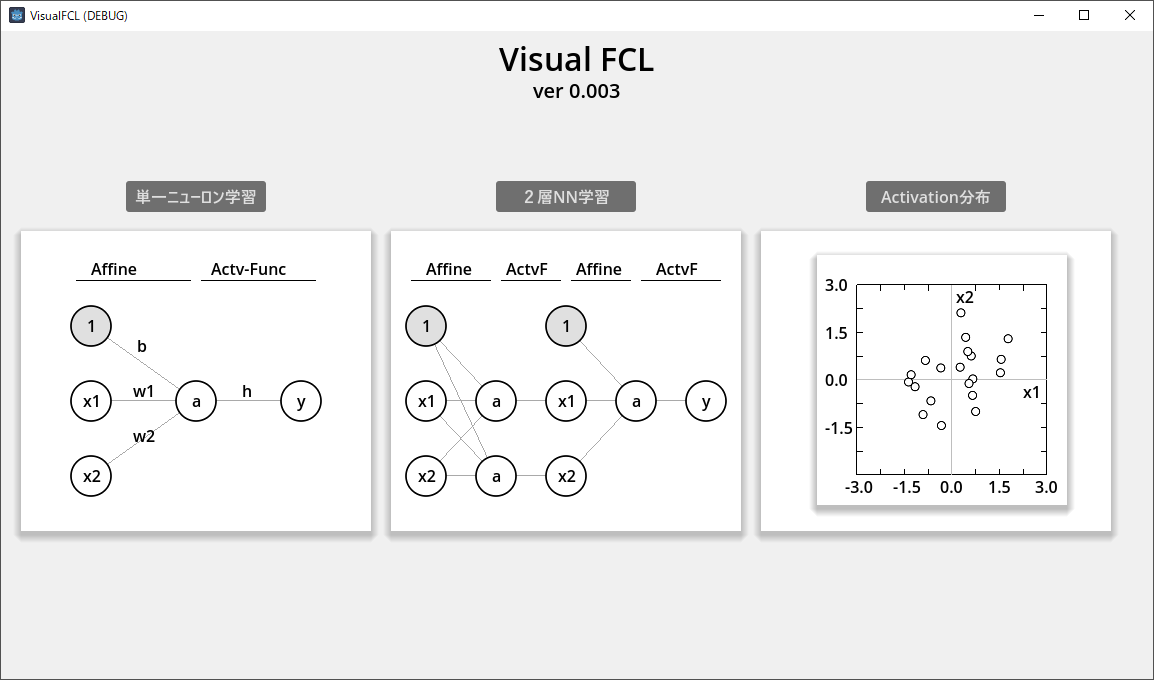
上図にアプリ起動時に表示されるトップシーンを示す。

version 0.003 では、単一NN（Neural Network、ニューラルネットワーク）学習、２層NN学習、およびアクティベーション分布を各種オプション・パラメータ値を指定して可視化可能。
それぞれのボタンまたはパネル部分を押下することで、それぞれのシーンに遷移する。

ダウンロード

単一ニューロン学習

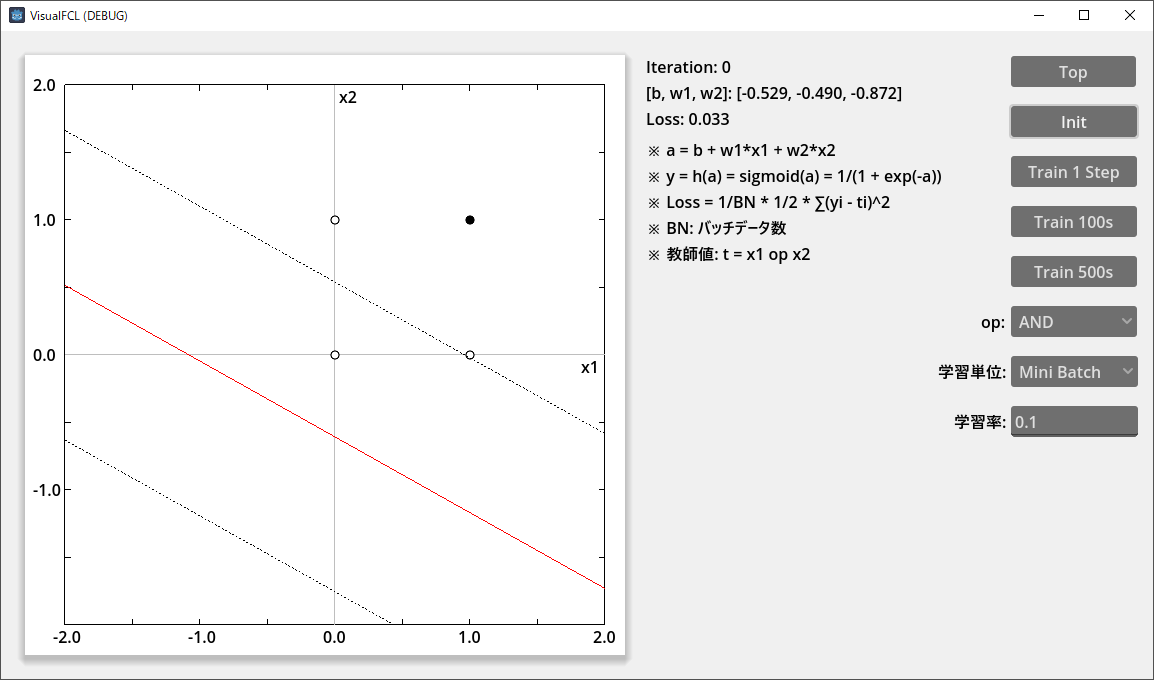
単一ニューロン学習シーンを上図に示す。

操作方法

右側に配置されているボタン押下で操作可能
「Top」：トップシーンに遷移
「Init」：重み（b, w1, w2）を初期化し、分離線（解説参照）を描画
「Train 1 Step」：学習を１ステップ行います。
「Train 100s」：学習を100ステップ行います。
「Train 500s」：学習を500ステップ行います。
「op」：教師値 t = x1 op X2 の演算子（op）を AND, OR, NAND, x1 > x2, XOR から選択可能
「学習単位」：データの学習単位をミニバッチ、オンライン、ランダム８回から選択可能
「学習率」：w1 -= α*∂L/w1 の学習率（α）を指定可能

解説

「ニューロン」とは生物の神経細胞を数学的およびプログラム的に取り扱いやすくモデル化したもの
生物の脳は多数の神経細胞から構成され、それぞれが他の神経細胞とシナプス結合し、情報処理を行う
本アプリでは、入力データ・分離線（後述）を２次元平面上に可視化するために、２入力ニューロンのみを取り扱う
※ 入力がN次元の場合、ひとつの入力はN次元空間の一点となる。
※ ひとつのニューロンの重みはN次元空間を２つに分割する N-1 次元超平面を表す。
ニューロンは、バイアス（b）・重み1, 2（w1, w2）の３つの状態変数を持つ
a = b + w1*x1 + w2*x2 を計算（これを数学的にはアフィン変換と呼ぶ）し、それに活性化関数に入力した結果を出力（y）とする。
活性化関数は変換を非線形にするためのもので、シグモイド関数、tanh() 関数、ReLU などが使用される
シグモイド関数：y = 1/(1+exp(-a))
ReLU: y = 0 if a < 0 else a
b + w1*x1 + w2*x2 = 0 とすると、x1, x2 空間で直線となる。これを分離線と呼ぶ（上図の赤い線）。
分離線上の点の出力は、活性化関数がシグモイドであれば 0.5、tanh() または ReLU であれば 0 となる。
グラフには b + w1*x1 + w2*x2 = ±1 の直線も破線で表示している。
活性化関数がシグモイドの場合、分離線上の出力値は 0.5, 破線上の出力値は 0.731, 0.269 となる。
単一ニューロンはデータを線形分離する能力を有する。
AND, OR などの線形分離可能な演算は正しく学習できるが、XOR などの線形分離不可能な演算を正しく学習することはできない。
損失 Loss = 1/N * 1/2∑(yi - ti)^2 と定義している
バックプロパゲーションにより、ニューロンの重み（b, w1, w2）を勾配降下法により学習している
バックプロパゲーションについては本稿では解説しないので、知らない人は自分でググレ

学習例

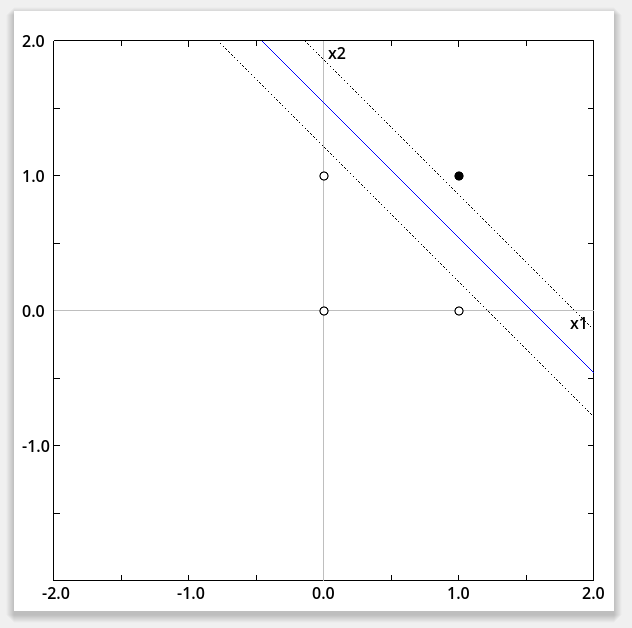
上図はAND演算を学習した結果（活性化関数：シグモイド）。教師値：1 の黒点と、0 の白点を直線により分離できている。
また、破線との間隔が狭まり、シグモイド関数が実質的にステップ関数に近づいている
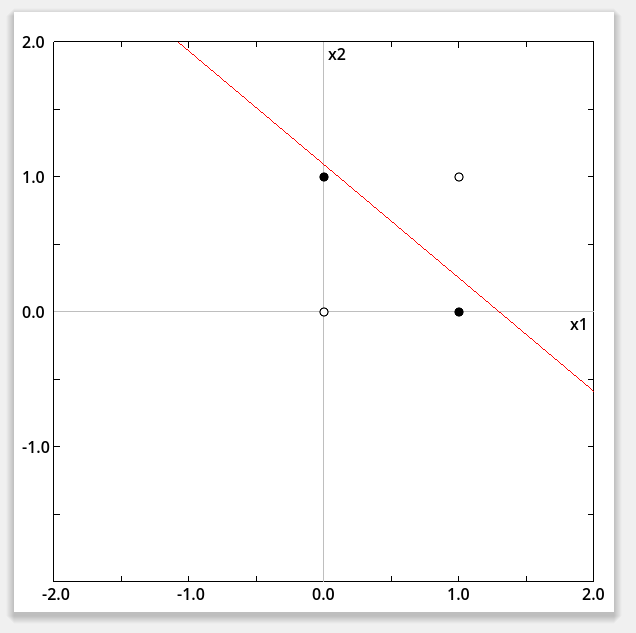
上図はXOR演算を千ステップ以上学習させてみた結果。教師値：1 の黒点と0の白点を線形分離不可能なので、Loss は大きいまま。

概要

ダウンロード

単一ニューロン学習

操作方法

解説

学習例

２層NN（ニューラルネット）学習

参考文献