【自前広告】筆者作成数独Webアプリ「さくさくナンプレ」
数々のおもてなし機能で、初心者でも問題がさくさく解けるよ。
問題難易度は「入門」「初級」「初中級」の3段階。
すべての問題が基本テクニックだけでロジカルに解けるよ。
「問題自動生成」「問題集」「今日の問題」の3つの遊び方ができるよ。

数独(Sudoku、ナンプレ、ナンバープレース)解き方(解法テクニック)
解き方基本テクニック
数独の解き方基本テクニックとしては、「フルハウス」「隠れたシングル」「裸のシングル」「ロックされた候補」があります。
これらのテクニックをマスターしておけば、かなり多くの問題を解くことができます。
まずは、これらをしっかり理解し、実際に使ってみてマスターしましょう。
フルハウス(Full House)
下図の1行目や左上の 3x3 ブロックのように、9箇所にうち8箇所が埋まっていると、残り1箇所は入ってない数字
(この場合は 5 と 4)に決まります。
このテクニックを「フルハウス(Full House)」と呼びます。
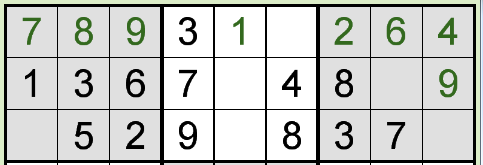
上図の例は横方向、3x3ブロックの場合ですが、縦方向の場合でも同じことです。
初心者のうちは、何が入ってない数字かがすぐにはわからず、1, 2, 3... と順に数えていくしかありませんが、 上級者になるとひと目みただけで、入っていない数字が瞬時にわかるようになるそうです。
隠れたシングル(Hidden Single)
下図のように、横方向の2つ、縦方向の2つのブロック全てに数字が入っている場合は、それらの数字の行・列にはその数字が入らないので、
残ったマス目にその数字が入ることが確定します。
このテクニックを「隠れたシングル(Hidden Single)」と呼びます。
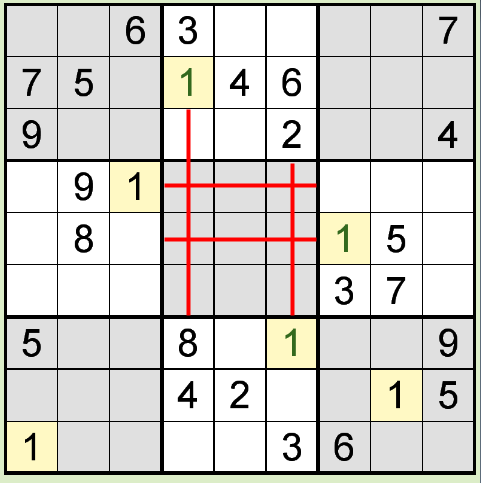
上図のように、横方向の2つ、縦方向の2つのブロック全てに数字が入っている場合は、ブロックが全て空でも必ず数字が確定します。 しかし、下図のように、ブロックに既に数字が入っていると、横方向・縦方向にその数字が入ってなくても数字が確定することがあります。
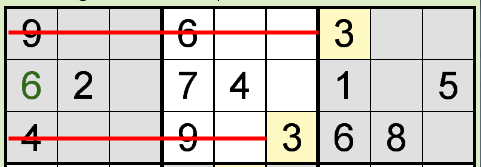
「隠れたシングル」は最もよく使われるテクニックです。 一説によれば、初中級問題ではこのテクニックを使うことで90%の数字を入れることが出来るそうです。
裸のシングル(Naked Single)
下図のように、ひとつの空欄に注目し、その空欄が属する行・列・ブロックに入っている数字を見ていくと、
使われていない数字がひとつだけの場合があります。その場合は、使われていない数字が入ることが確定します。
このテクニックを「裸のシングル(Naked Single)」と呼びます。
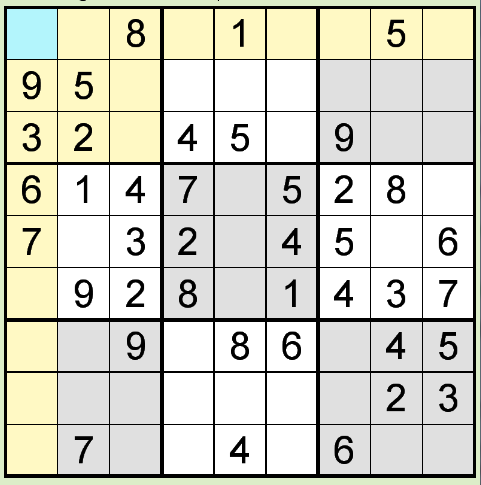
パズルの序盤で空欄が多い場合は、「裸のシングル」よりも前節の「隠れたシングル」で数字が決まることが多いです。 しかし、行・列・ブロックが埋まってくると、「隠れたシングル」では数字が決まらず、 「裸のシングル」のテクニックで決まることがよくあります。
ぱっと見で、入ってない数字を探すのは難しいですが、「さくさく解けるナンプレ(Sudoku)」には、 セル長押しで候補リストを表示する機能があります。これを使うと使われていない数字がすぐにわかるので、 詰まってしまって先に進めない場合は、使用してみるといいでしょう。
ロックされた候補(Locked Candidates)
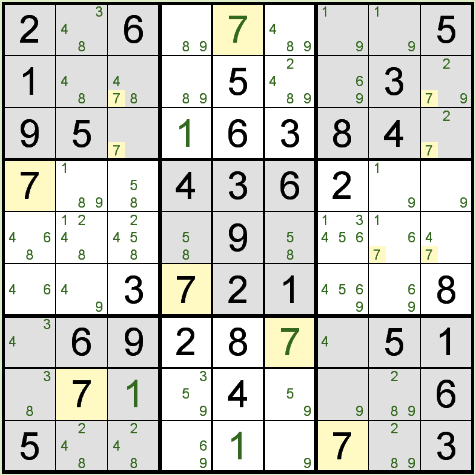
上図の右上ブロックの数字 7 に注目してください。
ブロック内で、7 は9列目にしかないので、2行9列目、または 3行9列目のどちらかに 7 が入ることになります。
したがって、4行目以降の9列目には、もう 7 は入らないので、右中央ブロック真ん中の 7 が確定となります。
このテクニックは「ロックされた候補(Locked Candidates)」と呼ばれます。
中級テクニック
X ウィング(X-Wing)
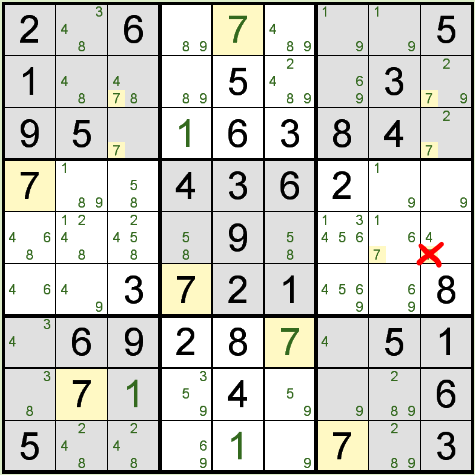
下図について、2 が入る箇所をよく見てください。
1列目には2が入る箇所が2行目、3行目の2箇所しかありません。
入る箇所が一箇所だけであれば、その位置に確定ですが、2箇所であれば、そのどちらかに入ることになります。
さらによく見ると、7列目も2が入る箇所が2行目、3行目の2箇所しかないことがわかると思います。 1列目と同様に、このどちらかに 2 が入ることになります。
このように、列(または行)に、ある数字が入る箇所が2箇所しかなく、それらが同じ行(または列)にある場合、 これを「X ウィング(X-Wing)」と呼びます。
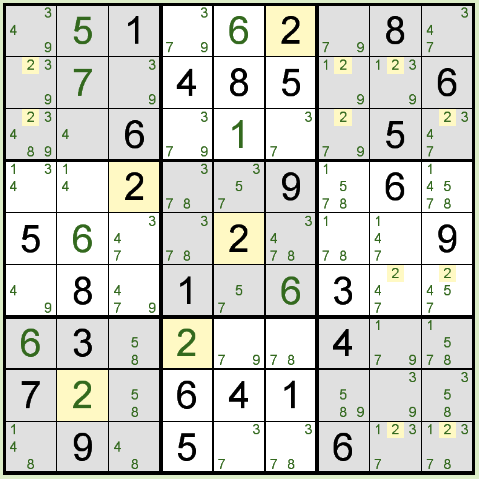
X ウィングがあると、2が入るパターンは、左上と右下、または左下と右上、の2パターンしかないので、
X ウィング以外の同じ行または列の他の箇所には 2 は入らないということになります。
上図のような場合では、下図のように右側の2箇所には 2 が入らないということが確定します。
この例の場合は、2 が入らないことがわかっても、直ぐにマス目の数字が確定するわけではありせんが、
地道に可能性を消していけば、やがて数字が確定することになります。
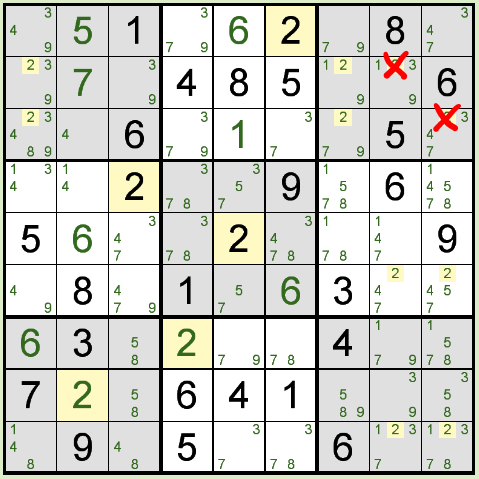
ちなみに、上図の右下部分にも 2 の X ウィングがあります。が、それにより消える部分は既に消している部分と同じです。
下図は、X ウィングにより数字が確定する例です。どこに何が入るかわかりますか?
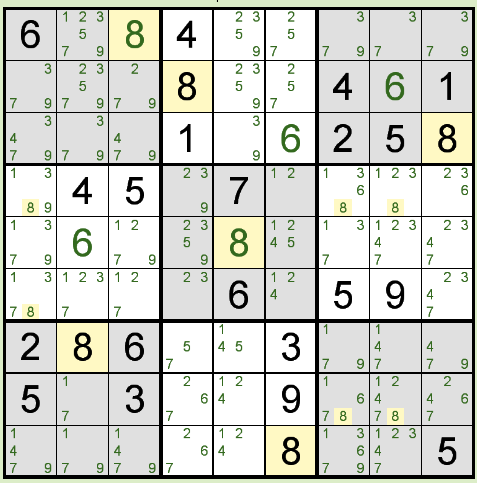
7,8列目、4,9行目の 8 が X ウィングになっています。よって、4行1列目には 8 は入らないことになり、 左中央ブロックに 8 が入る箇所は 6行1列目に確定します。
【自前広告】筆者作成数独Webアプリ「さくさくナンプレ」
数々のおもてなし機能で、初心者でも問題がさくさく解けるよ。
問題難易度は「入門」「初級」「初中級」の3段階。
すべての問題が基本テクニックだけでロジカルに解けるよ。
「問題自動生成」「問題集」「今日の問題」の3つの遊び方ができるよ。

